What Is An Adder?
An adder is a digital circuit that performs addition of numbers. In many computers and other kinds of processors adders are used in the arithmetic logic units or ALU. They are also used in other parts of the processor, where they are used to calculate addresses, table indices, increment and decrement operators and similar operations.
Although adders can be constructed for many number representations such as binary-coded decimal or excess-3, the most common adders operate on binary numbers. In case where two’s complement or ones ‘ complement is being used to represent negative numbers, it is trivial to modify an adder into an adder-subtractor. Other signed number representations require more logic around the basic adder.
Adders are basically classified into two types:
- Half Adder
- Full Adder
Other adder designs include the carry-select adder, conditional sum adder, carry-skip adder and carry-complete adder.
Half Adder
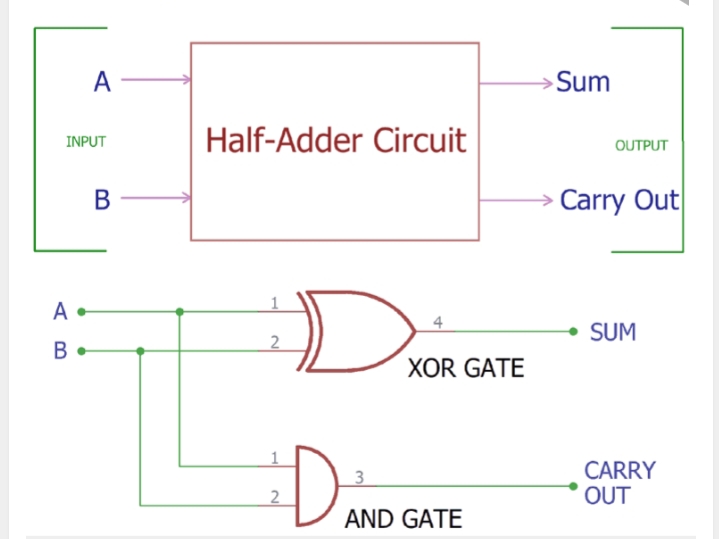
A half adder is a logical circuit that performs an addition operation on two binary digits. The half adder produces a sum and a carry value which are both binary digits. In other words, half adder adds two numbers and produces a sum bit (S) and carry bit (C) as the output. If A and B are the input bits, then sum bit (S) is the X-OR of A and B and the carry bit (C )will be the AND of A and B.
What You Need To Know About Half Adder
- Half Adder is a combinational logic circuit which adds two single binary digits and provides the sum and the carry bit.
- In half adder there are two input bits (A, B) which represent the data bits.
- Half adders are composed of single XOR and AND gate combination.
- In half adder, there is no previous carry bit as an input.
- Half adder has two outputs. One is the sum of the process (S) and the other is the carry of the summation (C ).
- It is used in calculators, computers, digital measuring devices etc.
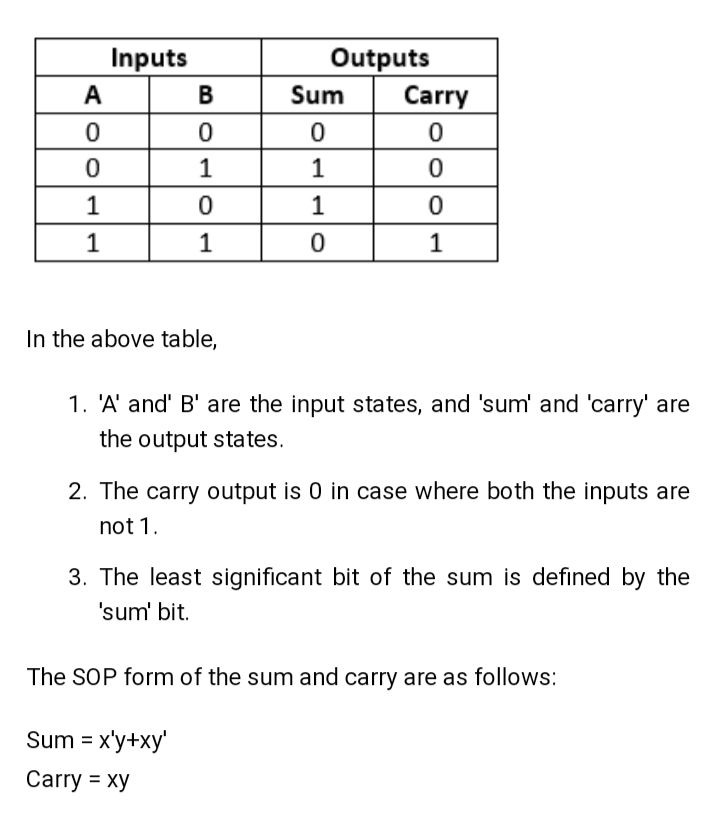
- Logical expression for half adder is: S=a⊕b ;C=a*b
Half Adder Circuit And Its Construction
Truth Table
Full Adder
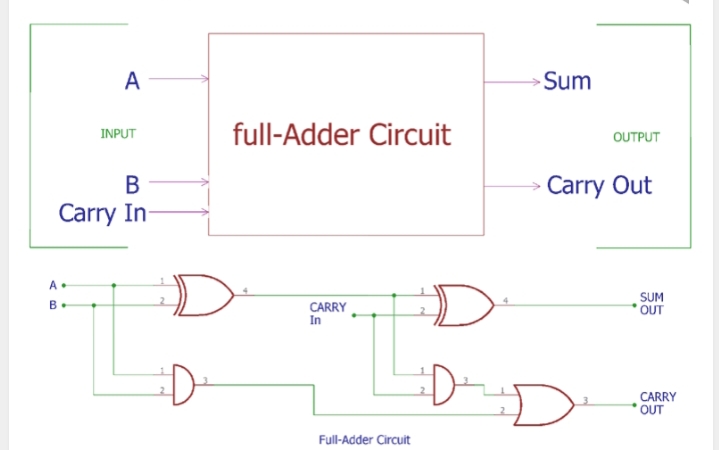
A full adder circuit is the central most digital circuit that performs addition and subtraction. It adds together two binary digits, plus a carry-in digit to produce a sum and a carry-out digit. It therefore has three inputs and two outputs. The first two inputs are A and B and the third input is an input carry as C-IN. The output carry is designated as C-OUT and the normal output is designated as S which is SUM.
A full adder logic is designed in such a manner that can take eight inputs together to create a byte-wide adder and cascade the carry bit from one adder to another.
What You Need To Know About Full Adder
- Full adder is combinational logical circuit that adds three one bit binary numbers that provide the sum and a carry bit.
- In full adder, there are three input bits (A, B, C-in).
- Full adder is composed of 3 AND, 2 XOR and 1 OR.
- In full adder, there is a previous carry bit as an output.
- The full adder has two outputs S and C.
- It is used in Multiple bit addition, digital processors etc.
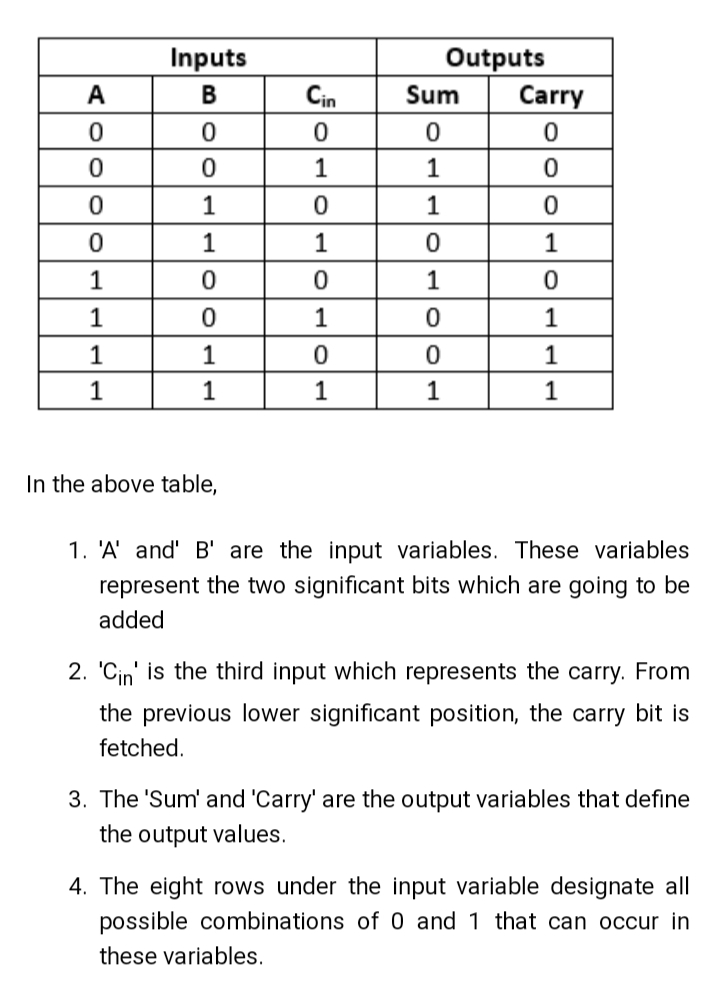
- Logical expression for full adder is: S=a⊕b⊕Cin; Cout=(a*b)+(Cin*(a⊕b))
Full Adder Circuit And Its Construction
Truth Table
Also Read: Difference Between Sequential And Combination Logic Circuits
Difference Between Half Adder And Full Adder In Tabular Form
| BASIS OF COMPARISON | HALF ADDER | FULL ADDER |
| Description | Half Adder is a combinational logic circuit which adds two single binary digits and provides the sum and the carry bit. | Full adder is combinational logical circuit that adds three one bit binary numbers that provide the sum and a carry bit. |
| Input | In half adder there are two input bits (A, B) which represent the data bits. | In full adder, there are three input bits (A, B, C-in). |
| Gate Combination | Half adders are composed of single XOR and AND gate combination. | Full adder is composed of 3 AND, 2 XOR and 1 OR. |
| Previous Carry Bit | In half adder, there is no previous carry bit as an input. | In full adder, there is a previous carry bit as an output. |
| Output | Half adder has two outputs. One is the sum of the process (S) and the other is the carry of the summation (C ). | The full adder has two outputs S and C. |
| Application | It is used in calculators, computers, digital measuring devices etc. | It is used in Multiple bit addition, digital processors etc. |
| Logical Expression | S=a⊕b ;C=a*b | S=a⊕b⊕Cin; Cout=(a*b)+(Cin*(a⊕b)) |
Also Read: Difference Between Half Wave And Full Wave Rectifier