In programming, data can be stored in data structures like graphs and trees. A tree is typically special form of graph i.e minimally connected graph and having only one path between any two vertices. In other words tree is a special case of graph having no loops, circuits and no-self loops. Graphs can have loops, circuits as well as can have self-loops.
Trees
Tree in data structures is a hierarchical data structure which stores information naturally in the form of hierarchy style. Trees are used to define data structures and as a basis for algorithms to solve problems. When compared to arrays, linked lists, stacks and queues which are linear data structures, a tree is a nonlinear data structure.
Just like a graph, a tree data structure is a collection of nodes. The nodes can then have children nodes. The children nodes can have their own children nodes referred to as grandchildren nodes. For example, the HTML DOM uses a tree data structure to represent the hierarchy of elements.
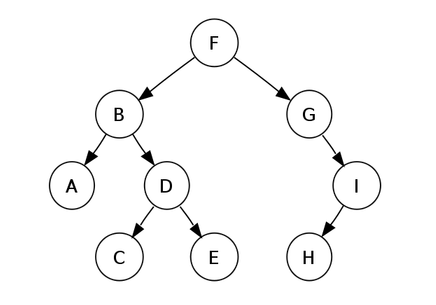
Terms Associated With Trees
- Root Node: This is the topmost node of the tree.
- Child: This is the node that is connected by parent nodes.
- Edge: Edges are used to connect two nodes.
- Parent Node: The root node in the structure having one or more than one reference node or pointing to other nodes.
- Leaf Node: This is the node that does not have any child in the structure.
- Level: A level can be regarded as the height of a tree. In tree, the height ascends from Top to bottom, where root node lay at 0 level and the leaf node lay at the bottom of a tree or subtree.
What You Need To Know About Trees (Properties)
- Tree is special form of graph i.e minimally connected graph and having only one path between any two vertices.
- Trees data structures are hierarchical, non-linear collections of linked nodes.
- In trees there are many rules/restrictions for making connections between nodes through edges.
- Different types of trees based different properties include binary tree, binary search tree, AVL tree, Heaps etc.
- Pre-order, in-order, and post-order are some kind of the logarithms that are used in trees to through all elements.
- An example of a tree is the HTML DOM where every other tag flows hierarchically from the html doctype tag.
- A tree cannot have a loop structure.
- Trees can be categorized as DAG (Directed Acyclic Graphs). DAG is a kind of directed graph that has no cycles.
- In trees there is parent-child relationship, every child can have only one parent and therefore, the flow can be from top to bottom direction or vice versa.
- In trees, there is exactly one root node and each child has only one parent.
- If trees have “n’’ vertices than it must have exactly “n-1’’ edges only.
- Trees are less complex when compared to graphs because they do not have cycles and self-loops but still connected.
- Tree is a special case of graph having no loops, no circuits and self-loops.
- Used in sorting, searching, traversing and binary search.
Graph
Graphs in JavaScript programming are a data structure comprising of a collection of nodes with edges. An edge is a pair of nodes that are connected. They are primarily used to describe a model that shows the route from one location to another location. A graph can be directed or undirected.
A directed graph contains edges which function similar to a one-way street. The edges flow from one node to another. For example you can have a graph of people and cars or TVs where each person can have several favorite cars or TVs but cars or TVs do not have a favorite person.
An undirected graph has edges which flow bi-directionally, similar to a two-lane road with traffic going both directions. For example, you can have a graph of goats whereby each goat has an owner and each owner has a goat.
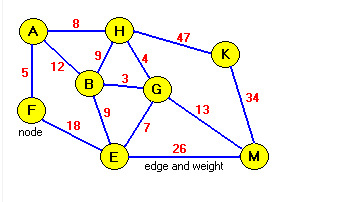
Terms Associated With Graph
- Cycle: This is a path where the first and the last vertices are same.
- Path: A path from a random vertex w is an adjacent sequence of vertices.
- Vertices: Vertices are the nodes present on the graph, connected with the help of edges.
- Degree: It is the number of edges incident on a vertex.
- Connected Graph: in case there is a path from a random vertex to any other vertex, then the graph can be described as connected Graph.
What You Need To Know About Graph (Properties)
- In graph there can be more than one path i.e graph can have uni-directional or bi-directional path (edges) between nodes.
- Graphs data structures are collections of linked nodes in non-linear network models.
- In graphs no restrictions/rules are there for connecting the nodes through edges.
- There are only two types of graphs based on different properties, that is, directed and Undirected Graphs.
- Breath First Search, Depth First Search are some kind of searching algorithms in graphs to traverse through each element.
- A good example of a network graph is a map of a road within a city.
- A graph can have a loop structure, which means the last element and the first element are same.
- Graph can be Cyclic or Acyclic.
- In graphs there is no parent-child relationship.
- There is no concept of root node in graphs.
- In graphs, the number of edges does not depend on the number of vertices.
- Graphs are more complex when compared to trees because it has cycles and loops.
- Graph can have loops, circuit as well as self-loops.
- Some applications of graph include coloring of maps, job scheduling, used in algorithms of data science and machine learning.
Also Read: Difference Between Binary Tree And Binary Search Tree
Difference Between Tree And Graph In Tabular Form
| BASIS OF COMPARISON | TREE | GRAPH |
| Description | Tree is special form of graph i.e minimally connected graph and having only one path between any two vertices. | In graph there can be more than one path i.e graph can have uni-directional or bi-directional path (edges) between nodes. |
| Structure | Trees data structures are hierarchical, non-linear collections of linked nodes. | Graphs data structures are collections of linked nodes in non-linear network models. |
| Rules/Restrictions | In trees there are many rules/restrictions for making connections between nodes through edges. | In graphs no restrictions/rules are there for connecting the nodes through edges. |
| Types | Binary tree, binary search tree, AVL tree, Heaps etc. | Directed and Undirected Graphs. |
| Search Algorithm | Pre-order, in-order, and post-order are some kind of the logarithms that are used in trees to through all elements. | Breath First Search, Depth First Search are some kind of searching algorithms in graphs to traverse through each element. |
| Example | An example of a tree is the HTML DOM where every other tag flows hierarchically from the html doctype tag. | A good example of a network graph is a map of a road within a city. |
| Loop Structure | A tree cannot have a loop structure. | A graph can have a loop structure, which means the last element and the first element are same. |
| Categories | Trees can be categorized as DAG (Directed Acyclic Graphs). DAG is a kind of directed graph that has no cycles. | Graph can be Cyclic or Acyclic. |
| Parent-Child Relationship | In trees there is parent-child relationship, every child can have only one parent and therefore, the flow can be from top to bottom direction or vice versa. | In graphs there is no parent-child relationship. |
| Concept of Root Node | In trees, there is exactly one root node and each child has only one parent. | There is no concept of root node in graphs. |
| Edges And Vertices | If trees have “n’’ vertices than it must have exactly “n-1’’ edges only. | In graphs, the number of edges does not depend on the number of vertices. |
| Complexity | Trees are less complex when compared to graphs because they do not have cycles and self-loops but still connected. | Graphs are more complex when compared to trees because it has cycles and loops. |
| Components | Tree is a special case of graph having no loops, no circuits and self-loops. | Graph can have loops, circuit as well as self-loops. |
| Application | Used in sorting, searching, traversing and binary search. | Some applications of graph include coloring of maps, job scheduling, used in algorithms of data science and machine learning. |
Comments are closed.