What Is A Binary Tree?
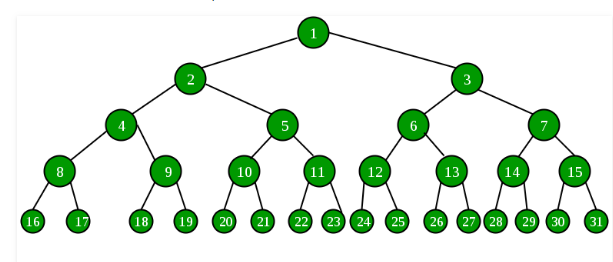
Incomputerscience, a binary tree is a hierarchical data structure in which each node has at most two children generally referred to as left child and the right child. Each node in a binary tree contains three nodes which include pointer to the left sub-tree, and pointer to the right sub-tree and data element. The topmost node in the tree is referred to as the root. Usually an empty tree is represented by NULL pointer.
Types of Binary Trees Based on structure
- Rooted binary tree (it has a root node and every node has not more than two children).
- Full binary tree (every node in the tree has either none or atmost 2 children).
- Degenerate tree (each parent node has only one child node. It behaves like a linked list).
- Perfect binary tree (all interior nodes have 2 children and leave have the same depth or same level.
- Complete binary tree (every level with exception of the last level is completely filled and all nodes are to the left periphery.
What You Need To Know About Binary Tree
- Binary tree is a hierarchical data structure in which a child can have zero, one or maximum two child nodes, each node contains a left pointer, a right pointer and a data element. There is no specific organization structure of the nodes in the tree.
- There are several types of binary trees, the most popular ones include: Full Binary Tree, Complete Binary Tree, Extended Binary Tree and Perfect Binary Tree.
- Common operations that can be performed on a binary tree are deletion, insertion, and transversal.
- Binary tree can also be described as a specialized form of tree which represents data in a tree structure. In a binary tree, the uppermost node represents the root pointer whereas the right and left root pointers represent data in a tree structure.
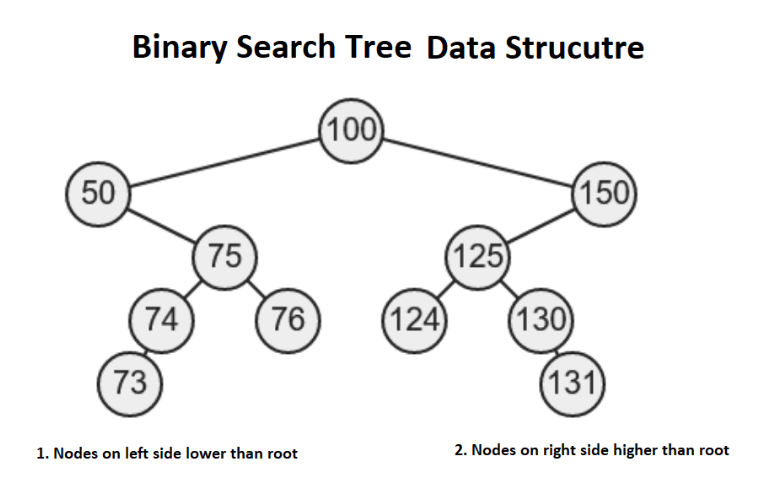
What Is Binary Search Tree?
In computer science, binary search trees are a useful data structure for fast addition and removal of data. Binary search tree is an organized binary tree in which there is a relative order in which nodes should be arranged. It is composed of nodes, which stores data and also links to up to two other child nodes. For a binary tree to be a binary search tree, the data of all the nodes in the left sub-tree of the root node should be less than the data of the root. The data of all nodes in the right sub-tree of the root node should be greater than equal to the data of the root. In this regard, the leaves on the farthest left of the tree have the lowest values, whereas the leaves on the right of the tree have the greatest values.
Types of binary Search Tree
- T-trees
- AVL trees
- Splay trees
- Tango trees
- Red-black trees
What You Need To Know About Binary Search Tree
- Binary search tree is an organized binary tree in which there is a relative order in which nodes should be arranged.
- The most popular types of binary search tree include: T-trees, AVL trees, Splay trees, Tango trees, Red-black trees etc.
- Binary search trees keep their keys sorted, therefore lookup usually implements binary search for operations. Binary search trees are more sorted binary trees that allows for fast and efficient lookup, insertion and deletion of items.
- Binary search tree can also be described as a type of binary tree in which all the nodes in the left sub-tree are less than or equal to the value of the root node and that of the right sub-tree are greater than or equal to the value of the root node.
Also Read: Difference Between Tree And Graph
Binary Tree Vs Binary Search Tree In Tabular Form
| BASIS COMPARISON | BINARY TREE | BINARY SEARCH TREE |
| Description | Binary tree is a hierarchical data structure in which a child can have zero, one or maximum two child nodes, each node contains a left pointer, a right pointer and a data element. There is no specific organization structure of the nodes in the tree. | Binary search tree is an organized binary tree in which there is a relative order in which nodes should be arranged. |
| Types | There are several types of binary trees, the most popular ones include: Full Binary Tree, Complete Binary Tree, Extended Binary Tree and Perfect Binary Tree. | The most popular types of binary search tree include: T-trees, AVL trees, Splay trees, Tango trees, Red-black trees etc. |
| Common Operations | Common operations that can be performed on a binary tree are deletion, insertion, and transversal. | Binary search trees keep their keys sorted, therefore lookup usually implements binary search for operations. Binary search trees are more sorted binary trees that allows for fast and efficient lookup, insertion and deletion of items. |
| Alternative Description | Binary tree can also be described as a specialized form of tree which represents data in a tree structure. In a binary tree, the uppermost node represents the root pointer whereas the right and left root pointers represent data in a tree structure. | Binary search tree can also be described as a type of binary tree in which all the nodes in the left sub-tree are less than or equal to the value of the root node and that of the right sub-tree are greater than or equal to the value of the root node. |
Advantages Of Trees (Binary & Binary Search Tree)
- Trees reflect structural relationships in the data.
- Trees provide an efficient insertion and searching.
- Trees are used to represent hierarchies.
- Trees are very flexible data, allowing to move sub-trees around with minimum effort.
Comments are closed.