Hypothesis testing is the art of testing if variation between two sample distributions can just be explained through random chance or not. Anytime we make a decision using statistics there are four possible outcomes, with two representing correct decisions and two representing errors. The errors are generally classified as type I and Type II errors. A type I error is the rejection of the true null hypothesis whereas type II error is the non-rejection of a false null hypothesis.
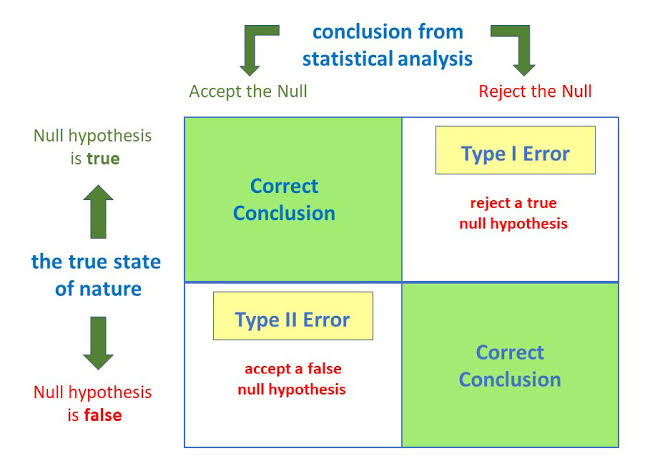
The chances of committing type I and type II errors are inversely proportional. What this means is, increasing the rate of type I error decreases the rate of type II error and vice versa.
What Is Type I Error?
Type I error, also known as a “false positive” is the error of rejecting a null hypothesis when it is actually true. In other words, this is the error of accepting an alternative hypothesis (the real hypothesis of interest) when the results can be attributed to chance. Plainly speaking, it occurs when we are observing a difference when in truth there is none (or more specifically – no statistically significant difference). So the probability of making a type I error in a test with rejection region R is P(R\H0 is true).
The probability of making a type I error is represented by your alpha level (α), which is the p-value below which you reject the null hypothesis. A p-value of 0.05 indicates that you are willing to accept a 5% chance that you are wrong when you reject the null hypothesis. You can reduce your risk of committing a type I error by using a lower value for p. For example, a p-value of 0.01 would mean there is a 1% chance of committing a Type I error.
Example of a Type I Error
Richard is a financial analyst. He runs a hypothesis test to discover whether there is a difference in the average price changes for large-cap and small-cap stocks. In the test, Richard assumes that the null hypothesis is that there is no difference in the average price changes between large-cap and small-cap stocks. Thus, his alternative hypothesis states that the difference between the average price changes does exist.
For the significance level, Richard chooses 5%. This means that there is a 5% probability that his test will reject the null hypothesis when it is actually true. If Richard’s test incurs a type I error, the results of the test will indicate that the difference in the average price changes between large-cap and small-cap stocks exists while there is no significant difference among the groups.
What You Need To Know About Type I Error
- A type 1 error is also known as a false positive and occurs when a researcher incorrectly rejects a true null hypothesis.
- A type I error also known as False positive.
- The probability that we will make a type I error is designated ‘α’ (alpha). Therefore, type I error is also known as alpha error.
- Type I error equals to the level of significance (α), ‘α’ is the so-called p-value.
- Type I error is associated with rejecting the null hypothesis.
- It is caused by luck or chance.
- The probability of Type I error reduces with lower values of (α) since the lower value makes it difficult to reject null hypothesis.
- Type I errors are generally considered more serious.
- It can be reduced by decreasing the level of significance.
- The probability of type I error is equal to the level of significance.
- It happens when the acceptance levels are set too lenient.
What Is Type II Error?
Type II error, also known as a “false negative” is the error of not rejecting a null hypothesis when the alternative hypothesis is the true state of nature. In other words, this is the error of failing to accept an alternative hypothesis when you don’t have adequate power. Plainly speaking, it occurs when we are failing to observe a difference when in truth there is one. So the probability of making a type II error in a test with rejection region R is 1-P(R/Hα is true). The power of the test can be P(R\Hα is true).
The type II error has an inverse relationship with the power of a statistical test. This means that the higher power of a statistical test, the lower the probability of committing a type II error. The rate of a type II error (i.e., the probability of a type II error) is measured by beta (β) while the statistical power is measured by 1- β.In other words, you can decrease your risk of committing a type II error by ensuring your test has enough power. You can do this by ensuring your sample size is large enough to detect a practical difference when one truly exists.
Example Of Type II Error
Amandla is a financial analyst. She runs a hypothesis test to discover whether there is a difference in the average price changes for large-cap and small-cap stocks. In the test, Amandla assumes as the null hypothesis that there is no difference in the average price changes between large-cap and small-cap stocks. Thus, her alternative hypothesis states that a difference between the average price changes does exist.
For the significance level, Amandla chooses 5%. This means that there is a 5% probability that her test will reject the null hypothesis when it is actually true. If Amandla’s test incurs a type II error, then the results of the test will indicate that there is no difference in the average price changes between large-cap and small-cap stocks. However, in reality, a difference in the average price changes does exist.
What You Need To Know About Type II Error
- A type II error does not reject the null hypothesis, even though the alternative hypothesis is the true state of nature. In other words, a false finding is accepted as true.
- A type II error also known as False negative. It is also known as false null hypothesis.
- Probability that we will make a type II error is designated ‘β’ (beta). Therefore, type II error is also known as beta error.
- Type II error equals to the statistical power of a test.
- Type II error equals to the statistical power of a test. The probability 1- ‘β’ is called the statistical power of the study.
- Type II error is associated with rejecting the alternative hypothesis.
- It is caused by a smaller sample size or a less powerful test.
- The probability of Type II error reduces with higher values of (α) since the higher value makes it easier to reject the null hypothesis.
- Type II errors are given less preference.
- It can be reduced by increasing the level of significance.
- The probability of type II error is equal to one minus the power of the test.
- It happens when the acceptance levels are set too stringent.
Difference Between Type I And Type II Error In Tabular Form
| BASIS OF COMPARISON | TYPE I ERROR | TYPE II ERROR |
| Description | A type 1 error is also known as a false positive and occurs when a researcher incorrectly rejects a true null hypothesis. | A type II error does not reject the null hypothesis, even though the alternative hypothesis is the true state of nature. In other words, a false finding is accepted as true. |
| Alternative Name | A type I error also known as False positive. | A type II error also known as False negative. It is also known as false null hypothesis. |
| Other Names | The probability that we will make a type I error is designated ‘α’ (alpha). Therefore, type I error is also known as alpha error. | Probability that we will make a type II error is designated ‘β’ (beta). Therefore, type II error is also known as beta error. |
| Equivalence | The probability of type I error is equal to the level of significance. | The probability of type II error is equal to one minus the power of the test. |
| Associated With | Type I error is associated with rejecting the null hypothesis. | Type II error is associated with rejecting the alternative hypothesis. |
| Cause | It is caused by luck or chance. | It is caused by a smaller sample size or a less powerful test. |
| Probability | The probability of Type I error reduces with lower values of (α) since the lower value makes it difficult to reject null hypothesis. | The probability of Type II error reduces with higher values of (α) since the higher value makes it easier to reject the null hypothesis. |
| Preference | Type I errors are generally considered more serious. | Type II errors are given less preference. |
| Reduction | It can be reduced by decreasing the level of significance. | It can be reduced by increasing the level of significance. |
| Occurence | It happens when the acceptance levels are set too lenient. | It happens when the acceptance levels are set too stringent. |