An image function f(x,y) must be digitized both spatially and in amplitude in order to become suitable for digital processing. Typically, a frame grabber or digitizer is used to sample and quantize the analogue video signal. Therefore, in order to create an image which is digital, we need to convert continuous data into digital form. This conversion from analog to digital involves two processes:
- Sampling (digitization of coordinate values).
- Quantization (digitization of amplitude values).
Sampling
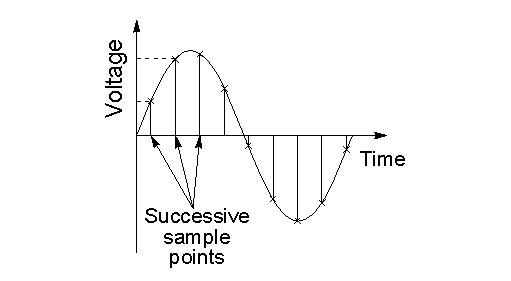
In digital image processing, sampling is the reduction of a continuous-time signal to a discrete-time signal. Sampling can be done for functions varying in space, time or any other dimension and similar results are obtained in two or more dimensions. Sampling takes two forms: Spatial and temporal. Spatial sampling is essentially the choice of 2D resolution of an image whereas temporal sampling is the adjustment of the exposure time of the CCD. Sampling is done on x-axis whereby infinite values are converted to digital values.
What You Need To Know About Sampling
- Sampling is the reduction of a continuous-time signal to a discrete-time signal.
- In sampling, the values on the y-axis, usually amplitude, are continuous but the time or x-axis is discretized.
- Sampling is done prior to the quantization process.
- The sampling rate determines the spatial resolution of the digitized image.
- Sampling reduces a continuous curve (Time-Amplitude Graph) to a series of “tent poles” over time.
- In the sampling process, a single amplitude value is selected from different values of the time interval to represent it.
Quantization
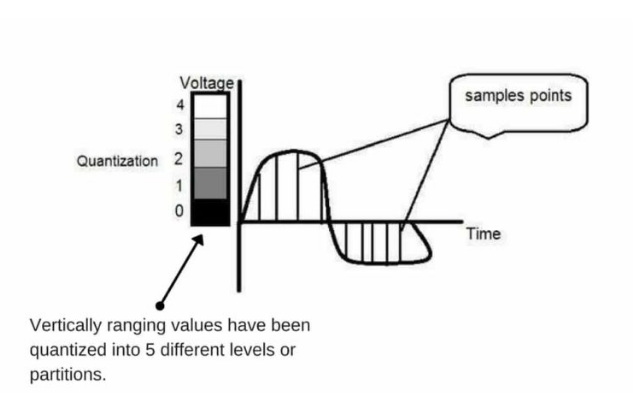
Quantization is the process of mapping input values from a large set to output values in a smaller set, often with a finite number of elements. Quantization is the opposite of sampling. It is done on the y-axis. When you are quantizing an image, you are actually dividing a signal into quanta (partitions). On the x axis of the signal, are the coordinate values and on the y-axis, we have amplitudes. Therefore, digitizing the amplitudes is what is referred to as quantization.
What You Need To Know About Quantization
- The transition between continuous values of the image function and its digital equivalent is referred to as quantization.
- Quantization makes a sampled signal truly digital and ready for processing by a computer.
- In quantization, time or x-axis is continuous and the y-axis or amplitude is discretized.
- Quantization is done after sampling process.
- The quantization level determines the number of grey levels in the digitized image.
- Quantization reduces a continuous curve to a continuous series of ‘’stair steps’’ that exist at regular time interval.
- In quantization process, the values representing the time intervals are rounded off, to create a defined set of possible amplitude values.
Difference Between Sampling And Quantization In Tabular Form
| BASIS OF COMPARISON | SAMPLING | QUANTIZATION |
| X And Y axis | In sampling, the values on the y-axis, usually amplitude, are continuous but the time or x-axis is discretized. | In quantization, time or x-axis is continuous and the y-axis or amplitude is discretized. |
| When It Is Done | Sampling is done prior to the quantization process. | Quantization is done after sampling process. |
| Resolution | The sampling rate determines the spatial resolution of the digitized image. | The quantization level determines the number of grey levels in the digitized image. |
| Effect On A Continuous Curve | Sampling reduces a continuous curve (Time-Amplitude Graph) to a series of “tent poles” over time. | Quantization reduces a continuous curve to a continuous series of ‘’stair steps’’ that exist at regular time interval. |
| Values Representing The Time Intervals | In the sampling process, a single amplitude value is selected from different values of the time interval to represent it. | In quantization process, the values representing the time intervals are rounded off, to create a defined set of possible amplitude values. |