In computer science, a search algorithm is an algorithm (if more than one, algorithms) designed to solve a search problem. Search algorithms work to retrieve information stored within particular data structure, or calculated in the search space of a problem domain, with either discrete or continuous values.
There are different types of searching algorithm, some of them are as follows :
- Linear Search
- Binary Search
- Jump Search
- Interpolation Search
- Exponential Search
- Sublist Search (Search a linked list in another list)
- Fibonacci Search
- The Ubiquitous Binary Search
In this article, find more details about the linear search and binary search and the comparison between these two algorithms.
What Is Linear Search?
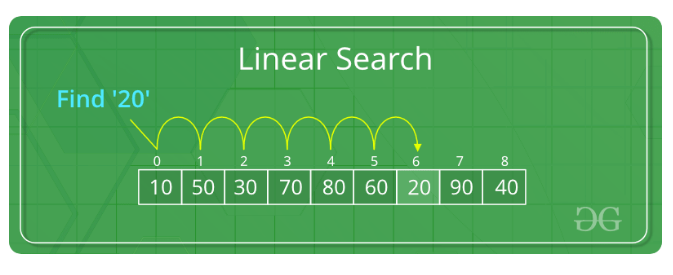
Linear search also referred to as sequential search is the simplest searching algorithm that searches for an element in a list in sequential order. It relies on the technique of traversing a list from start to end by exploring properties of all the elements that are found on the way. Linear sear is mostly very simple to implement and is practical when the list has only a few elements or when performing a single search in an un-ordered list (list which the items are not sorted).
Linear search is implemented using the following steps:
Step 1- Read the search element from the user
Step 2- Compare the search element with the first element in the list.
Step 3- If both are matched, then display ‘’given element is found’’ and terminate the function.
Step 4- if both are not matched, then compare search element with the next element in the list.
Step 5- Repeat steps 3 and 4 until search element is compared with last element in the list.
Step 6- if last element in the list also doesn’t match, then display ‘’Element is not found’’ and terminate the function.
Advantages of a linear search
- Will perform fast searches of small to medium lists. With today’s powerful computers, small to medium arrays can be searched relatively quickly.
- The list does not need to sorted. Unlike a binary search, linear searching does not require an ordered list.
- Not affected by insertions and deletions. As the linear search does not require the list to be sorted, additional elements can be added and deleted. As other searching algorithms may have to reorder the list after insertions or deletions, this may sometimes mean a linear search will be more efficient.
What Is Binary Search?
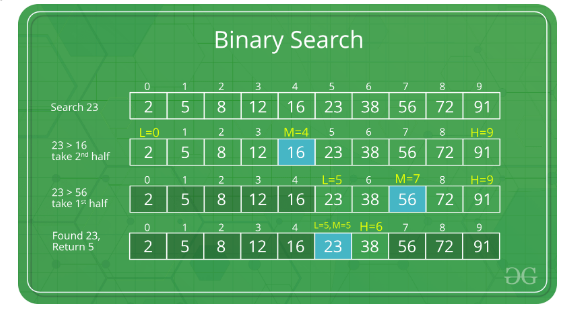
Binary search is an efficient algorithm for finding an item from a sorted list of items. It works by repeatedly dividing in half the portion of the list that could contain the item, until you have narrowed the possible locations to just one. One of the most common ways to use binary search is to find an item in a sorted array or list of large size. It’s time complexity makes it very fast as compared to other sorting algorithms.
Binary search algorithm works on the principle of divide and conquer. One of the major limitations of binary search is that the array or list of elements must be sorted for the algorithm to work on it.
Binary search looks for a particular item by comparing the middle most item of the collection. If a match occurs, then the index of item is returned. If the middle item is greater than the item, then the item is searched in the sub-array to the left of the middle item. Otherwise, the item is searched for in the sub-array to the right of the middle item. This process continues on the sub-array as well until the size of the sub-array reduces to zero.
Also Read: Difference Between Binary Tree And Binary Search Tree
Advantages of Binary Search
- Binary search works efficiently on sorted data no matter the size of the data
- Instead of performing the search by going through the data in a sequence, the binary algorithm randomly accesses the data to find the required element. This makes the search cycles shorter and more accurate.
- Binary search performs comparisons of the sorted data based on an ordering principle than using equality comparisons, which are slower and mostly inaccurate.
- After every cycle of search, the algorithm divides the size of the array into half hence in the next iteration it will work only in the remaining half of the array.
Difference Between Linear Search And Binary Search In Tabular Form
| Points of comparison | Linear search | Binary search |
|---|---|---|
| Definition | The linear search starts searching from the first element and compares each element with a searched element till the element is not found. | It finds the position of the searched element by finding the middle element of the array. |
| Sorted data | In a linear search, the elements don’t need to be arranged in sorted order. | The pre-condition for the binary search is that the elements must be arranged in a sorted order. |
| Implementation | The linear search can be implemented on any linear data structure such as an array, linked list, etc. | The implementation of binary search is limited as it can be implemented only on those data structures that have two-way traversal. |
| Approach | It is based on the sequential approach. | It is based on the divide and conquer approach. |
| Size | It is preferrable for the small-sized data sets. | It is preferrable for the large-size data sets. |
| Efficiency | It is less efficient in the case of large-size data sets. | It is more efficient in the case of large-size data sets. |
| Worst-case scenario | In a linear search, the worst- case scenario for finding the element is O(n). | In a binary search, the worst-case scenario for finding the element is O(log2n). |
| Best-case scenario | In a linear search, the best-case scenario for finding the first element in the list is O(1). | In a binary search, the best-case scenario for finding the first element in the list is O(1). |
| Dimensional array | It can be implemented on both a single and multidimensional array. | It can be implemented only on a multidimensional array. |
Applications of Search Algorithms
Specific applications of search algorithms include:
- In game theory and especially combinatorial game theory, choosing the best move to make next (such as with the minmax algorithm)
- Finding a combination or password from the whole set of possibilities
- Factoring an integer (an important problem in cryptography)
- Optimizing an industrial process, such as a chemical reaction, by changing the parameters of the process (like temperature, pressure, and pH)
- Retrieving a record from a database
- Finding the maximum or minimum value in a list or array
- Checking to see if a given value is present in a set of values.
Key Takeaways
- Linear Search is defined as a sequential search algorithm that starts at one end and goes through each element of a list until the desired element is found, otherwise the search continues till the end of the data set. It is the easiest searching algorithm
- Binary search compares the target value to the middle element of the array. If they are not equal, the half in which the target cannot lie is eliminated and the search continues on the remaining half, again taking the middle element to compare to the target value, and repeating this until the target value is found. If the search ends with the remaining half being empty, the target is not in the array.
- In a linear search, it is not required to sort the array before searching the element. However, in a binary search, it is necessary to sort the array before searching the element.
- The time complexity of a linear search is O(N) while the time complexity of a binary search is O(log2N).
- The process of linear search can be worked upon any linear data structure like a double linked list, linked list, and vector. On the other hand, the process of binary search can be worked on the data structures that have two-way traversal, which is backward traversal and forward traversal.
- Linear search can be used on both single and multidimensional array, whereas the binary search can be implemented only on the one-dimensional array.
- Binary search is suitable for a large data set as it takes less time. Linear search is not suitable for the large data set.