Scalar and vector quantities used to be a thorough subject of debate among physicists for many years. It took a lot of studies and papers for a clear difference between the two quantities to emerge. These days it is quite easy to make a distinction between a scalar and a vector quantity.
Scalar Quantity
Scalar quantity is defined by only one element referred to as magnitude, without which there is no scalar quantity. Therefore, a scalar is usually said to be a physical quantity that only has magnitude and no other characteristics. Magnitude means the size of the quantity such as length or strength.
A scalar is any number that gives the size or magnitude of a quantity, therefore a unit of measurement must be attached to the number like degrees or meters. Any random number is not a scalar. For example number 25 is meaningless unless you tell us that 25 is a measurement of something like distance or time or temperature.
What You Need To know About Scalar Quantity
- Scalar quantity implies that the physical quantity has only magnitude and no direction.
- Any change in scalar quantity indicates only change in magnitude of the concerned physical quantity.
- Scalar quantities are always one dimensional.
- The scalar quantity can divide another scalar quantity.
- Scalar quantity follows ordinary rules of algebra. Therefore, normal algebraic method can be used to solve scalar quantity.
- Any mathematical calculation/operation between two or more scalar quantities will always result to a scalar quantity.
- Any mathematical operation between a scalar quantity and a vector quantity will always result to a vector quantity.
- Scalar quantity cannot be resolved; it has exactly same value in all directions.
Examples of Scalar Quantities
- Speed
- Work
- Distance
- Power
- Temperature
- Volume
- Charge
- Gravitational potential
- Frequency
- Energy
- Length
- Kinetic energy
- Specific heat
- Power
- Calorie
- Density
- Entropy
Vector Quantity
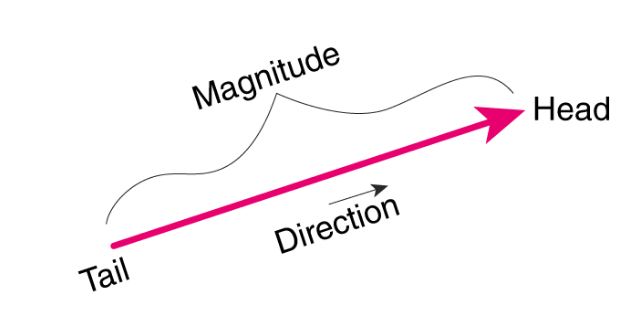
A vector quantity can be defined by two elements, magnitude and direction. Without these two elements a physical quantity cannot be defined as a vector. Therefore, a vector quantity can be defined as a physical quantity that comprises of both magnitude and direction. Magnitude means the size of the quantity such as length or strength. Direction means the position where the vector is pointing to or where it is being directed such as left or right, east, west, north or south (up or down).
When a vector is drawn, it is represented by an arrow whose length represents the vector’s magnitude and whose arrow head points in the direction of the vector.
What You Need To know About vector Quantity
- Vector quantity implies that the physical quantity comprise of both magnitude and direction.
- Any change in vector quantity indicates changes either in magnitude or in direction or in both.
- Vector quantities can be either one or two or three dimensional.
- Two vectors cannot be divided or can never divide.
- Vector rules follows rules of any mathematical operation. Geometry method can be used to solve vector quantity.
- Mathematical operation between two or more vector quantities may give either vector or scalar quantity.
- Mathematical operation between vector and scalar quantities will result to a vector quantity.
- Vector quantity can be resolved in two mutually perpendicular directions using the adjacent angle.
Examples Of Vector Quantities
- Force
- Acceleration
- weight
- Shearing Stress
- velocity
- Electric field intensity
- Centrifugal force
- Torque
- Momentum
- Electric flux
Quantities That Are Both Vector And Scalar
- Mass
- Weight
- Speed
- Work
- Power
- Energy
- Displacement
- Distance
- Force
- Torque
Also Read: Difference Between Mass And Weight
Difference Between Scalar And Vector Quantity In Tabular Form
| BASIS OF COMPARISON | SCALAR QUANTITY | VECTOR QUANTITY |
| Description | Scalar quantity implies that the physical quantity has only magnitude and no direction. | Vector quantity implies that the physical quantity comprise of both magnitude and direction. |
| Change | Any change in scalar quantity indicates only change in magnitude of the concerned physical quantity. | Any change in vector quantity indicates changes either in magnitude or in direction or in both. |
| Dimensional | Scalar quantities are always one dimensional. | Vector quantities can be either one or two or three dimensional. |
| Division Of Quantity | The scalar quantity can divide another scalar quantity. | Two vectors cannot be divided or can never divide. |
| Mathematical Rules | Scalar quantity follows ordinary rules of algebra. | Vector rules follows rules of any mathematical operation. |
| Mathematical Operation Between Two or More Quantities | Any mathematical calculation/operation between two or more scalar quantities will always result to a scalar quantity. | Mathematical operation between two or more vector quantities may give either vector or scalar quantity. |
| Mathematical Operation Between A Scalar Quantity And A Vector Quantity | Any mathematical operation between a scalar quantity and a vector quantity will always result to a vector quantity. | Mathematical operation between vector and scalar quantities will result to a vector quantity. |
| Direction | Cannot be resolved; it has exactly same value in all directions. | Can be resolved in two mutually perpendicular directions using the adjacent angle. |
What Are Some Of The Similarities Between Scalar Quantity And Vector Quantity
- Both have some specific unit and dimension.
- Both scalar and vector have magnitude.
- Both scalar and vector quantity are measurable.
- Both can express certain physical quantity.
- Mathematical operation between vector and scalar quantities will result to a vector quantity.
Comments are closed.