In mathematical analysis and approximation, Taylor series and Taylor polynomials are used to represent functions in different contexts. While these mathematical constructs are almost the same, their purposes, applications and fundamental characteristics are different. Let’s talk about them.
What is Taylor Series?
A Taylor series is an infinite sum of terms that represents a function as an expansion around a specific point. It is named after the mathematician Brook Taylor. The general form of a Taylor series for a function f(x) centered at the point a is given by:
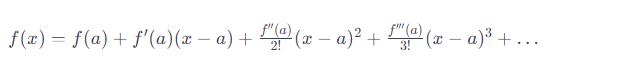
In other words, the Taylor series expresses a function as an infinite sum of terms, each term being a derivative of the function evaluated at the center point a, divided by the corresponding factorial, multiplied by the power of (x−a). The series includes terms from the first derivative to higher-order derivatives.
The representation is often written more compactly using the sigma notation:

In other words,
- f(x) = Real or complex-valued function, that is infinitely differentiable at a real or complex number “a” is the power series
- n = Total number of terms in the series
A Taylor series is also called a Maclaurin series when 0 is the point where the derivatives are considered, named after Colin Maclaurin, who made extensive use of this special case of Taylor series in the mid-18th century.
Taylor series is used in calculus and analysis to represent functions as infinite sums, allowing for the approximation and analysis of functions around specific points. They are particularly useful in understanding the local behavior of functions, especially in the vicinity of the center point a.
What is Polynomial Series?
A Taylor polynomial is a finite sum of terms obtained from a Taylor series, representing an approximation of a function around a specific point. The Taylor polynomial is obtained by truncating the Taylor series after a certain number of terms. The general form of an n-th degree Taylor polynomial for a function f(x) centered at the point a is given by:
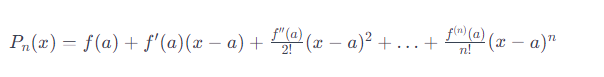

The Taylor polynomial is used in numerical analysis, engineering, and other applied fields. The higher the degree of the polynomial (n), the more accurate the approximation within a certain range around the center point. However, the accuracy is limited to the degree of the polynomial, and the approximation becomes less reliable as one moves farther from the center point.
Taylor Series And Taylor Polynomial: Key Differences
| Feature | Taylor Series | Taylor Polynomial |
|---|---|---|
| Definition | Infinite sum of terms representing a function at a point and its derivatives at that point. | Finite sum of terms derived from the Taylor series, often truncated to a certain degree. |
| Representation | Infinite series: f(x)=f(a)+f′(a)(x−a)+f′′(a)2!(x−a)2+f′′′(a)3!(x−a)3+… | Finite polynomial: Pn(x)=f(a)+f′(a)(x−a)+f′′(a)2!(x−a)2+…+fn(a)n!(x−a)n |
| Convergence | May converge or diverge based on the function and x values in the series. | Generally converges within a specific interval, depending on the polynomial degree. |
| Length of Series/Polynomial | Infinite number of terms. | Finite, determined by the chosen degree of the polynomial. |
| Representation Purpose | Theoretical representation of a function for a wide range of x values. | Practical approximation of a function within a limited range. |
| Application | Used in theoretical mathematics and analysis. | Widely used in numerical analysis, engineering, physics, and applied fields. |
| Degree of Approximation | Infinite terms provide an exact representation of the function within the convergence interval. | Higher degrees provide better approximations, but accuracy is limited to the polynomial degree. |
| Usage in Practice | Often not used directly in practical applications due to the infinite terms. | Frequently used for numerical calculations, curve fitting, and simplifying functions for computational efficiency. |