When it comes to digital electronics and sequential logic circuits, counters play an important role in a number of applications. They serve as indispensable components for tasks such as counting, frequency division, and synchronization. Among the various counter types available, two prominent contenders often stand out: the Ring Counter and the Johnson Counter. Both of these circuits exhibit unique characteristics and capabilities that make them valuable in specific scenarios.
This article tries to explain in the most simple way, the key difference between ring and Johnson counter, in the context of their design principles, operational modes, and practical implementations.
Ring Counter
A Ring Counter is a type of digital counter circuit that operates in a cyclic manner, where the output of one flip-flop is connected as the input to the next flip-flop in the sequence. This creates a “ring” of connected flip-flops, hence the name “Ring Counter.” The counter cycles through a predefined sequence of states, and only one flip-flop output is high at any given time.
In other words, a ring counter is a type of counter composed of flip-flops connected into a shift register, with the output of the last flip-flop fed to the input of the first, making a ‘’circular’’ or ‘’ring’’ structure.
The most common implementation of a Ring Counter is with D-type flip-flops. In this configuration, the output of each flip-flop is fed into the clock input of the next flip-flop in the ring. To initiate the counter, an initial state is loaded into one of the flip-flops, and subsequently, the high output moves through the connected flip-flops, one step at a time, in a circular fashion.
The Ring Counter’s operation is self-sustaining, making it simple and easy to design. However, it has a limitation: it requires an external mechanism to load the initial state into the counter, which can be cumbersome and inconvenient in some applications. To address this issue, the Johnson Counter was developed as a variation of the Ring Counter.
One of the primary applications of a Ring Counter is in creating time delays, where the delay time is determined by the number of flip-flops in the ring. It can also be used for generating specific sequences in applications such as control systems, pattern recognition, and even in some types of shift registers.
One of the most crucial characteristics of a Ring Counter is its maximum count or the number of states it can sequence through. For an ‘n’-bit Ring Counter, the maximum count is ‘n’ (equal to the number of flip-flops). Therefore, it is often not ideal for applications requiring large counting sequences.
There are two types of ring counters:
- Straight ring counter-connects the output of the last shift register to the first shift register input and circulates a single one (or zero) bit around the ring.
- Twisted ring counter-connects the complement of output of the last shift register to the input of the first register and circulates a stream of ones followed by zeros around the ring.

What You Need To Know About Ring Counter
- Ring counter is mostly used in successive approximation type ADC and stepper motor control.
- In ring counter, the output of the last flip flop is connected to the input of the first flip flop.
- Decoding is easy in ring counter as the number of states is equal to the number of flip flops.
- If ‘n’ is the number of flip flops that is used in ring counter, the number of possible states is ‘n’. That means the number of states is equal to the number of flip flops used.
- In ring counter, if input frequency is f in ring counter then the output is f/n.
- The total number of unused states in the ring counter is (2^n-n).
Johnson Counter
A Johnson Counter is a specialized type of digital counter circuit that overcomes some of the limitations of the Ring Counter. It is also known as a “Twisted Ring Counter” or “Walking Ring Counter” due to its unique operation. Like the Ring Counter, it is a sequential logic circuit that cycles through a sequence of states, but it does so in a different manner.
In other words, Johnson counter is a modified ring counter, where the inverted output from the last flip flop is connected to the input to the first. It is referred to as Inverse Feedback Counter. The register cycles through a sequence of bit-patterns. The MOD of the Johnson counter is 2n if n flip-flops are used. The main advantage of the Johnson counter is that it only needs half the number of flip-flops compared to the standard ring counter for the same MOD.
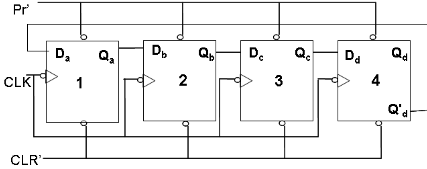
The key feature that sets the Johnson Counter apart is its ability to provide a one-hot encoded output. In a one-hot state, only one flip-flop output is high (1), while all other outputs are low (0). This characteristic makes the Johnson Counter particularly useful in applications where individual state detection is required or where precise control over specific states is essential.
The Johnson Counter is constructed using D-type flip-flops as well, but unlike the Ring Counter, it employs a feedback mechanism that connects the complement (inverted) output of the last flip-flop to the input of the first flip-flop, forming a loop. This feedback arrangement allows the Johnson Counter to move through its sequence in both directions: forwards and backwards. This bidirectional capability is a valuable advantage over the unidirectional nature of the Ring Counter.
The counter’s state sequence follows a specific pattern, which is a combination of high (1) and low (0) outputs. For an ‘n’-bit Johnson Counter, the sequence length is 2n, meaning it can cycle through twice as many states as there are flip-flops. Consequently, Johnson Counters are capable of handling larger counting sequences than Ring Counters of the same size.
The one-hot encoded output of a Johnson Counter simplifies state decoding, making it easier to interpret and use the counter’s output in applications such as pattern recognition, error detection, and control systems. Additionally, the bidirectional operation opens up possibilities for applications where back-and-forth movement through the sequence is beneficial.
However, the complexity of the Johnson Counter increases with the number of flip-flops, and its implementation may require more hardware compared to the Ring Counter. Despite this, its versatility and ability to handle larger count sequences often make it a preferred choice in various practical scenarios.
What You Need To Know About Johnson Counter
- Johnson counter is also referred to as walking counter or switching tail counter and is mostly used in phase shift or function generator.
- In Johnson counter, the output bar or Q-bar of the last flip flop is connected to the input of the first flip flop.
- Decoding Johnson counter is complex as compared to ring to counter.
- If ‘n’ is the number of flip flop used in Johnson counter, then the total number of states used is ‘2n’.
- In Johnson counter, if input frequency is ‘f’ then the output is ‘f/2n’.
- The total number of unused states in Johnson counter is (2^n-2n).
Also Read: Difference Between GM Counter And Scintillation Counter
Difference Between Ring Counter And Johnson Counter In Tabular Form
| BASIS OF COMPARISON | RING COUNTER | JOHNSON COUNTER |
| Application | Ring counter is mostly used in successive approximation type ADC and stepper motor control. | Johnson counter is also referred to as walking counter or switching tail counter and is mostly used in phase shift or function generator. |
| Output | In ring counter, the output of the last flip flop is connected to the input of the first flip flop. | In Johnson counter, the output bar or Q-bar of the last flip flop is connected to the input of the first flip flop. |
| Decoding | Decoding is easy in ring counter as the number of states is equal to the number of flip flops. | Decoding Johnson counter is complex as compared to ring to counter. |
| Number Of Flip-Flops Vs Number Of Possible States Used | If ‘n’ is the number of flip flops that is used in ring counter, the number of possible states is ‘n’. That means the number of states is equal to the number of flip flops used. | If ‘n’ is the number of flip flop used in Johnson counter, then the total number of states used is ‘2n’. |
| Input Frequency | In Johnson counter, if input frequency is ‘f’ then the output is ‘f/2n’. | In Johnson counter, if input frequency is ‘f’ then the output is ‘f/2n’. |
| Unused States | The total number of unused states in Johnson counter is (2^n-2n). | The total number of unused states in Johnson counter is (2^n-2n). |
Key Difference
- Operation:
- A Johnson counter is a type of shift register where the output of the last stage is fed back to the input of the first stage. It circulates a sequence of 0s and 1s, generating a unique pattern for each state.
- A ring counter is also a type of shift register, but it circulates a single 1 bit among the stages, resulting in only one stage being high (1) while the others are low (0) in each state.
- Output States:
- In a Johnson counter with ‘n’ stages, the counter goes through 2n states before repeating. It has 2n possible output states, providing a wider range of sequences.
- A ring counter with ‘n’ stages only has n possible output states, as only one stage is high (1) at a time. This results in a more limited set of output sequences.
- Number of Flip-Flops:
- A Johnson counter requires 2n flip-flops for ‘n’ stages since it needs to store both the current state and its complement.
- A ring counter only requires ‘n’ flip-flops for ‘n’ stages, as it circulates a single 1 bit among them.
- Applications:
- Johnson counters are often used for applications that require a sequence of unique states, such as in frequency division, time delay generation, and pseudo-random number generation.
- Ring counters are frequently used in applications where generating a single high output among several stages is needed, such as in decoding operations, selecting specific functions, and creating time delays.