Difference Between Quick Sort And Merge Sort

What Is Merge Sort?

Merge sort is an efficient, general-purpose, comparison-based sorting algorithm. Merge sort is a divide and conquer algorithm that was invented by John von Neumann in 1945. Most implementations produce a stable sort, which means that if two elements have the same value, they hold same relative position in the output as they did in the input. In other words, the relative order of elements with equal values is preserved in the sorted output.

Merge sort repeatedly breaks down a list into several sublists until each sublist consists of a single element and merging those sublists in a manner that results into a sorted list. Merge sort is a comparison sort, meaning, it can sort any input for which a less-than relation is defined.

Running time is an import factor thing to consider when selecting a sorting algorithm since efficiency is often thought of in terms of speed. Merge sort runs in a guaranteed O(n log n) time, which is significantly faster than the average and worst case running times of several other sorting algorithms.

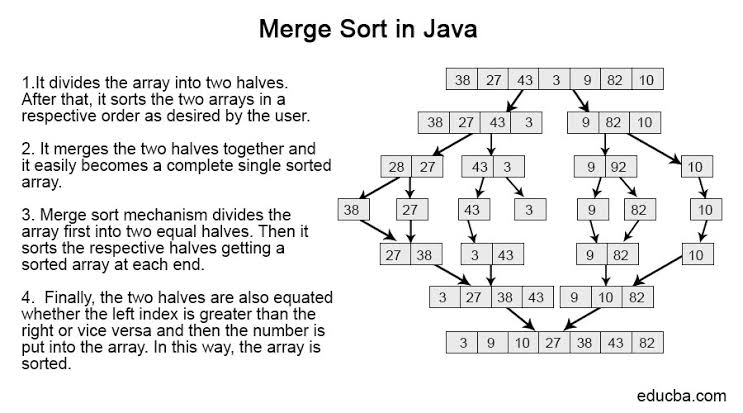
What You Need To Know About Merge Sort

In the merge sort, the array is parted into two halves (n/2).
The worst case complexity of quick sort is O(n2) as there is need of lot of comparisons in the worst condition.
Merge sort can work well on any type of data sets irrespective of its size (whether large or small).
The merge sort is an external sorting method in which the data that is to be sorted cannot be accommodated in the memory at the same time and some has to be kept in the auxiliary memory.
Merge sort is more efficient and works faster than quick sort in case of larger array size or datasets.
Merge sort is preferred for linked lists.
Merge sort is not in place because it requires additional memory space to store the auxiliary arrays.
Merge sort does not exhibit a good cache locality and this makes merge sort slower when compared to quick sort.
Merge sort is stable as two elements with equal value appear in the same order in sorted output as they were in the input unsorted array.

What Is Quick Sort?

Quick sort also referred to as partition-exchange sort is an efficient sorting algorithm. Developed by British computer scientist Tony Hoare in 1959 and published in 1961,it is still a commonly used algorithm for sorting. When implemented well, it can be about two or three times faster than its main competitors, merge sort and heapsort.

Quick sort is a divide-and-conquer algorithm. It works by selecting a ‘pivot’ element from the array and partitioning the other elements into two sub-arrays, according to whether they are less than or greater than the pivot. The sub-arrays are then sorted recursively. This can be done in-place, requiring small additional amounts of memory to perform the sorting.

Quick sort is a comparison sort, meaning that it can sort items of any type for which a “less-than” relation (formally, a total order) is defined. Efficient implementations of Quick sort are not a stable sort, meaning that the relative order of equal sort items is not preserved.

Mathematical analysis of quick sort shows that, on average, the algorithm takes O(n log n) comparisons to sort n items. In the worst case, it makes O(n²) comparisons, though this behavior is rare.

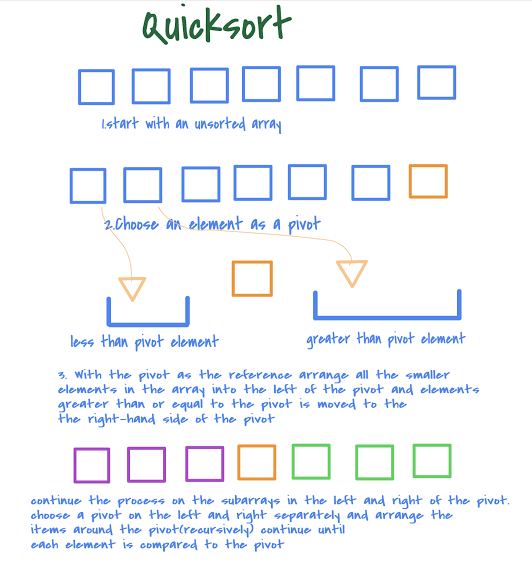
What You Need To Know About Quick Sort

In quick sort, the array is parted into any ratio. There is no compulsion of dividing the array of elements into equal parts.
The worst case complexity in merge sort is O(n log n).
The quick sort cannot work well with large datasets.
The quick sort is internal sorting method where the data that is to be sorted is adjusted at a time in main memory.
Quick sort is more efficient and works faster than merge sort in case of smaller array size or datasets.
Quick sort is preferred for arrays.
The quick sort doesn’t require any additional storage.
Quick sort exhibits good cache locality and this makes quick sort faster than merge sort in many cases like in virtual memory environment.
Quick sort is unstable; however it can be made stable by implementing some changes in the code.

Also Read: Difference Between Array And Pointer

Difference Between Quick Sort And Merge Sort In Tabular Form

BASIS OF COMPARISON	MERGE SORT	QUICK SORT
Description	In the merge sort, the array is parted into two halves (n/2).	In quick sort, the array is parted into any ratio. There is no compulsion of dividing the array of elements into equal parts.
Worst Case Complexity	The worst case complexity of quick sort is O(n2) as there is need of lot of comparisons in the worst condition.	The worst case complexity in merge sort is O(n log n).
Working	Merge sort can work well on any type of data sets irrespective of its size (whether large or small).	The quick sort cannot work well with large datasets.
Sorting	The merge sort is an external sorting method in which the data that is to be sorted cannot be accommodated in the memory at the same time and some has to be kept in the auxiliary memory.	The quick sort is internal sorting method where the data that is to be sorted is adjusted at a time in main memory.
Efficiency	Merge sort is more efficient and works faster than quick sort in case of larger array size or datasets.	Quick sort is more efficient and works faster than merge sort in case of smaller array size or datasets.
Use	Merge sort is preferred for linked lists.	Quick sort is preferred for arrays.
Additional Storage	Merge sort is not in place because it requires additional memory space to store the auxiliary arrays.	The quick sort doesn’t require any additional storage.
Speed	Merge sort does not exhibit a good cache locality and this makes merge sort slower when compared to quick sort.	Quick sort exhibits good cache locality and this makes quick sort faster than merge sort in many cases like in virtual memory environment.
Stability	Merge sort is stable as two elements with equal value appear in the same order in sorted output as they were in the input unsorted array.	Quick sort is unstable; however it can be made stable by implementing some changes in the code.