What Is NP Problem?
An NP problem, short for Non-deterministic Polynomial time problem, is a class of decision problems in theoretical computer science. The class NP contains problems for which a proposed solution can be verified in polynomial time, meaning that given a solution, there exists a polynomial-time algorithm to check whether the solution is correct or not.
For example If I claim that there is a polynomial time solution for a particular problem, you ask me to prove it. Then, I will give you a proof which you can easily verify in polynomial time. Note that, here we are not talking about whether there is a polynomial time solution for this problem or not. But we are talking about verifying the solution to a given problem in polynomial time.
To answer the rest of question, you first need to understand which NP-hard problems are also NP-complete. If an NP-hard problem belongs to set NP, then it is NP-complete. To belong to set NP, a problem needs to be:
(i) A decision problem,
(ii) The number of solutions to the problem should be finite and each solution should be of polynomial length, and
(iii) Given a polynomial length solution, we should be able to say whether the answer to the problem is yes/no.
Key Aspects of NP Problems
- Decision Problems: NP problems are a subset of decision problems, which means they have a yes-or-no answer. For a given input, the problem seeks to determine whether the answer is “yes” or “no” based on a certain criterion.
- Verification in Polynomial Time: For an NP problem, if someone claims to have found a solution, it can be efficiently verified by a deterministic algorithm in polynomial time. In other words, if the solution is correct, it can be checked relatively quickly. However, finding the solution itself might not be straightforward and could be computationally challenging.
- Non-deterministic Aspect: The name “non-deterministic” comes from a theoretical model of computation where a non-deterministic Turing machine can guess the correct solution in a single step. It doesn’t mean that non-deterministic machines are more powerful than deterministic machines in practice; it’s just a theoretical concept.
- Existence of Solutions: NP problems are about recognizing whether a solution exists for a given input, rather than finding the actual solution.
What Is NP Complete Problem?
As a special class of decision problems within the complexity class NP (Non-deterministic Polynomial time), NP-complete problems are among the most challenging problems in computer science and have the property that if any one of them can be solved in polynomial time (P-time), then all problems in NP can be solved in polynomial time. In other words, NP-complete problems represent the hardest problems in NP with respect to polynomial-time reductions.
A polynomial-time reduction is a way to transform one problem into another in such a way that solving the second problem allows us to solve the first problem efficiently. More formally, if we can transform problem A into problem B in polynomial time, and we can efficiently solve problem B, then we can use this transformation to efficiently solve problem A.
In other words, NP-Complete is a complexity class which represents the set of all problems X in NP for which it is possible to reduce any other NP problem Y to X in polynomial time.
Intuitively this means that we can solve Y quickly if we know how to solve X quickly. Precisely, Y is reducible to X, if there is a polynomial time algorithm f to transform instances y of Y to instances x = f(y) of X in polynomial time, with the property that the answer to y is yes, if and only if the answer to f(y) is yes.
A problem is considered NP-complete if it satisfies two conditions:
- It is in the class NP, which means a proposed solution can be verified in polynomial time.
- It is NP-hard, which means it is at least as hard as the hardest problems in NP. This implies that any problem in NP can be polynomial-time reduced to the NP-complete problem.
NP-complete problems are often referred to as “the hardest problems in NP” because any problem in NP can be reduced to an NP-complete problem in polynomial time. This property is known as “completeness” in the context of computational complexity.
The concept of NP-completeness was introduced by Stephen Cook and Leonid Levin in the 1970s, and its study has had some impact on theoretical computer science. The discovery of NP-complete problems led to the recognition of a large class of problems that are likely to be inherently difficult to solve efficiently.
Example
3-SAT. This is the problem wherein we are given a conjunction (ANDs) of 3-clause disjunctions (ORs), statements of the form
(x_v11 OR x_v21 OR x_v31) AND
(x_v12 OR x_v22 OR x_v32) AND
... AND
(x_v1n OR x_v2n OR x_v3n)
where each x_vij is a boolean variable or the negation of a variable from a finite predefined list (x_1, x_2, ... x_n).
It can be shown that every NP problem can be reduced to 3-SAT. The proof of this is technical and requires use of the technical definition of NP (based on non-deterministic Turing machines). This is known as Cook’s theorem.
What makes NP-complete problems important is that if a deterministic polynomial time algorithm can be found to solve one of them, every NP problem is solvable in polynomial time (one problem to rule them all).
Also Read: Difference Between Deterministic And Non-deterministic Algorithms
What Is NP Hard Problem?
As a class of computational problems, an NP-hard problem is a problem for which a polynomial-time algorithm has not been found to solve it. It does not necessarily belong to the class NP, and it may or may not have polynomial-time verifiable solutions. The key point is that any problem in NP can be polynomial-time reduced to an NP-hard problem.
In simple terms. These are at least as hard as the hardest problems in NP. Unlike NP problems, NP-hard problems do not necessarily have polynomial-time verifiable solutions. In other words, there is no known polynomial-time algorithm to verify whether a proposed solution is correct or not for an NP-hard problem. If we can solve these problems in polynomial time, we can solve any NP problem that can possibly exist.
The precise definition here is that a problem X is NP-hard, if there is an NP-complete problem Y, such that Y is reducible to X in polynomial time.
But since any NP-complete problem can be reduced to any other NP-complete problem in polynomial time, all NP-complete problems can be reduced to any NP-hard problem in polynomial time. Then, if there is a solution to one NP-hard problem in polynomial time, there is a solution to all NP problems in polynomial time.
Example
The halting problem is an NP-hard problem. This is the problem that given a program P and input I, will it halt? This is a decision problem but it is not in NP. It is clear that any NP-complete problem can be reduced to this one. As another example, any NP-complete problem is NP-hard.
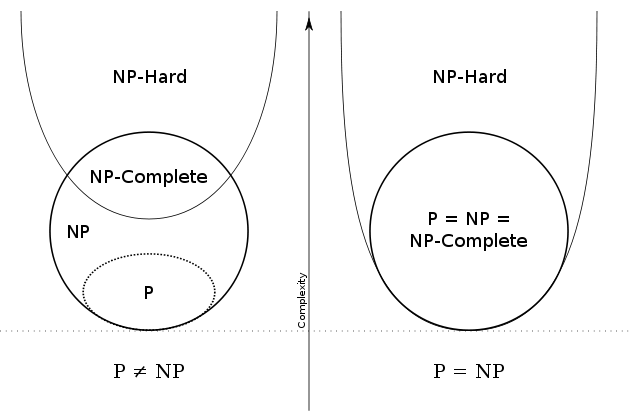
The concept of NP-hardness is essential in computational complexity theory because it identifies a set of problems that are unlikely to have efficient solutions (i.e., solutions that can be computed in polynomial time). If an NP-hard problem could be solved in polynomial time, it would imply that all problems in NP can be solved in polynomial time, which would mean P = NP.
Also Read: Difference Between P And NP Problems
Examples of NP-hard and NP-complete problems
NP-hard problems
- Traveling Salesman Problem (TSP): Given a list of cities and distances between them, determine if there exists a route that visits each city exactly once and returns to the starting city, with a total distance less than or equal to a given value.
- Boolean Satisfiability Problem (SAT): Given a Boolean formula, determine whether there exists an assignment of truth values to the variables that makes the formula true.
- Knapsack Problem: Given a set of items, each with a weight and a value, and a maximum weight capacity for a knapsack, determine the most valuable combination of items that can be placed in the knapsack without exceeding its capacity.
NP-complete problems
- Boolean Satisfiability Problem (SAT): Given a Boolean formula, determine if there exists an assignment of truth values to the variables that makes the formula true.
- Vertex Cover Problem: Given an undirected graph, find the smallest set of vertices such that every edge in the graph is incident to at least one vertex in the set.
- 3-SAT: A specific variant of the SAT problem, where the Boolean formula is in conjunctive normal form (CNF) and each clause contains exactly three literals.
- Subset Sum Problem: Given a set of integers and a target sum, determine whether there exists a subset of the integers that adds up to the target sum.
NP Hard vs NP Complete Problem In Tabular Form
| Basis | NP Hard | NP Complete |
| Definition | A problem is considered NP-hard if it is at least as hard as the hardest problems in the class NP (Non-deterministic Polynomial time). In other words, if a polynomial-time algorithm exists for solving an NP-hard problem, it would imply P = NP. | A problem is NP-complete if it is both NP-hard and also belongs to the class NP. In other words, an NP-complete problem has a polynomial-time algorithm for verification (solution checking) and is among the hardest problems in NP. |
| Verification complexity | There is no known polynomial-time algorithm to verify a solution to an NP-hard problem. | Solutions to NP-complete problems can be verified in polynomial time. |
| Solvability | It is not known whether NP-hard problems can be solved in polynomial time (P-time). They may or may not have polynomial-time algorithms. | NP-complete problems are in NP and have the property that if any one of them can be solved in polynomial time, then all problems in NP can be solved in polynomial time (P = NP). |
| Subset relationship | NP-hard problems are a superset of NP problems. They include problems that may or may not be in NP. | NP-complete problems are a subset of NP-hard problems. They represent the hardest problems in NP. |
| Reductions | NP-hard problems can be polynomial-time reduced to each other. If problem A is NP-hard and there exists a polynomial-time reduction from A to problem B, then B is also NP-hard. | NP-complete problems are the most challenging problems in NP with respect to polynomial-time reductions. Any problem in NP can be polynomial-time reduced to an NP-complete problem. |
| Examples | The Traveling Salesman Problem (TSP) and the Boolean Satisfiability Problem (SAT) are examples of NP-hard problems. | The SAT problem itself is an NP-complete problem, and many other problems, such as the Vertex Cover problem and the Knapsack problem, are also NP-complete. |
| Importance | NP-hard problems represent a broad class of computational problems that are difficult to solve efficiently. | NP-complete problems provide a useful set of benchmark problems for studying computational complexity and the relationships between different classes of problems. |
| Complexity class | NP-hard problems are not specifically categorized within the complexity classes NP, P, or co-NP. | NP-complete problems belong to the class NP, which consists of decision problems that can be verified in polynomial time |
In the study of computational complexity, the question of whether NP problems can be solved efficiently (in polynomial time) has been one of the most difficult open problems in computer science and mathematics, known as the P vs. NP problem.
Resolving this question has unprecedented implications for many fields, including cryptography, optimization, artificial intelligence, medicine etc. As of today 2023, P vs. NP remains an unsolved problem, and it is not known whether NP problems can be efficiently solved (P-time) or not.