Hyperbola
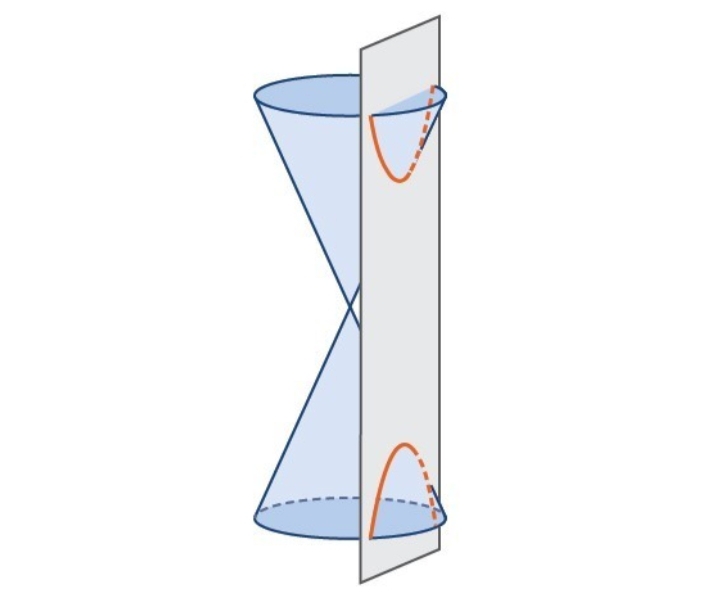
A hyperbola is a conic section formed by intersecting a right circular cone with a plane at an angle such that both halves of the cone are intersected. This intersection produces two separate unbounded curves that are mirror images of each other. In other words, a hyperbola is a conic section formed by the intersection of a cone with a plane that intersects the base of the cone and is not tangent to the cone.
Like the ellipse, the hyperbola can also be described as a set of points in the coordinate plane. A hyperbola is the set of all points (x, y) in a plane such that the difference of the distances between (x, y) and the foci is a positive constant. Hyperbolas have applications to a number of different systems and problems including sundials and trilateration.
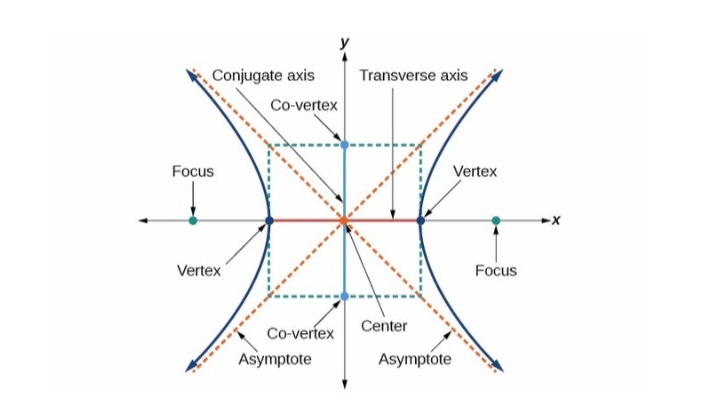
All hyperbolas share common features, and it is possible to determine the specifics of any hyperbola from the equation that defines. A hyperbola consists of two curves, each with a vertex and a focus. The transverse axis is the axis that crosses through both vertices and foci, and the conjugate axis is perpendicular to it. A hyperbola also has asymptotes which cross in an ‘’x’’. The two branches of the hyperbola are on opposite sides of the asymptotes’ cross. The vertices and asymptotes can be used to form a rectangle, with the vertices at the centers of two opposite sides and the corners on the asymptotes. The centers of the other two sides, along the conjugate axis, are called the co-vertices. Where the asymptotes of the hyperbola cross is called the center.
Facts About Hyperbola
- A hyperbola can be described as the difference of distances between a set of points, which are present in a plane to two fixed points is a positive constant.
- A hyperbola is a disconnected curve with only one branch.
- A hyperbola results from intersection of the plane and the cone, but with the plane at an orientation that is not parallel to the side of the cone.
- A hyperbola has two foci and two directrix.
- A hyperbola has an accentricity value greater than one.
- The hyperbolas can be of different shapes.
- The hyperbola curves open more widely than that of parabolas.
- The hyperbola has two curves that mirror each other and open in opposing sides.
- A hyperbola has two asymptotes.
- The arms present in hyperbola are not parallel to each other.
- The general equation of a hyperbola is written as x2/a2-y2/b2=1
- Hyperbolas are used in various applications in today’s world including the path followed by the shadow of a sundial, the shape of an open orbit, it is also used as an arch in many constructed buildings, as equations in mathematics, physics, engineering, geometry etc.
Parabola
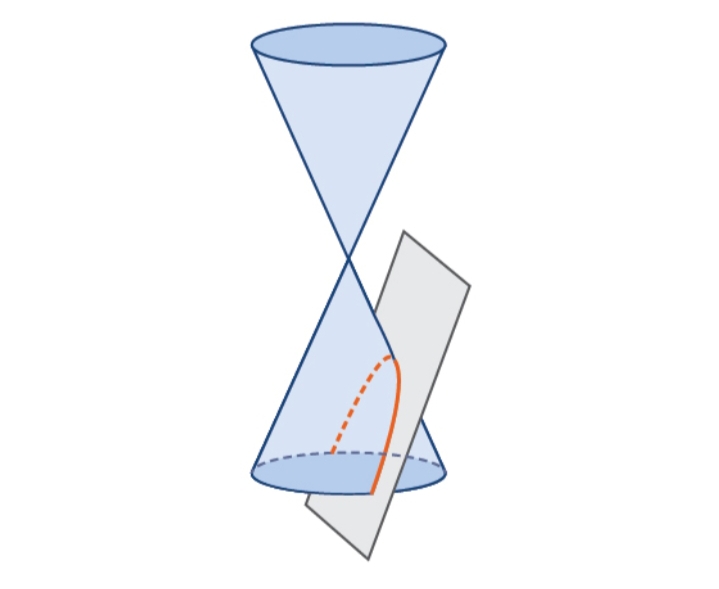
A parabola is an open curve or a conic section produced by the intersection of a right circular cone and a plane parallel to an element of the cone. As a plane curve, it may be defined as the path (locus) of a point moving so that its distance from a fixed line (the directrix) is equal to its distance from a fixed point (the focus).
Like the ellipse and hyperbola, the parabola can also be defined by a set of points in the coordinate plane. A parabola is the set of all points (x, y) in a plane that are the same distance from a fixed line, called the directrix and a fixed point (the focus) not on the directrix.
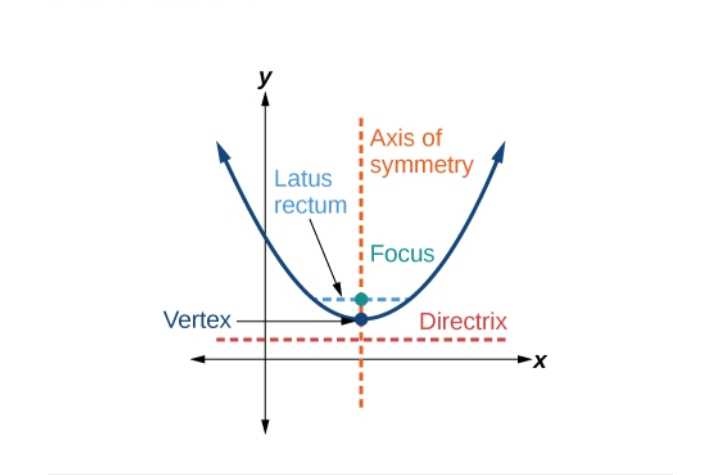
The vertex of the parabola is the point on the curve that is closest to the directrix; it is equidistant from the directrix and the focus. The vertex and the focus determine a line, perpendicular to the directrix that is the axis of the parabola. The line through the focus parallel to the directrix is the latus rectum (straight side). The endpoints of the lactus rectum lie on the curve. The parabola is symmetric about its axis, moving farther from the axis as the curve recedes in the direction away from its vertex.
Facts About Parabola
- A parabola can be described as a set of points in a plane which are equidistant from a straight line or directrix and focus.
- A parabola is a connected curve with only one branch.
- A parabola is created when a plane cuts a conical surface parallel to the side of the cone.
- A parabola has single focus and directrix.
- Parabola has an accentricity value of one. Accentricity is equal to the distance of the point on the curve to the fixed point divided by the perpendicular distance of that same point on the curve to the fixed line.
- All parabolas should have the same shape irrespective of the size.
- The parabola curves open less widely than that of hyperbola.
- The parabola has only one curve.
- A parabola has no asymptotes.
- The two arms present in a parabola should be parallel to each other.
- The general equation of a parabola is y=ax2.
- Parabolas are used in various applications such as automobile headlight reflectors, design of ballistic missiles etc. They also play a major role in physics, engineering, mathematics etc.
Difference Between Hyperbola And Parabola In Tabular Form
| BASIS OF COMPARISON | HYPERBOLA | PARABOLA |
| Description | A hyperbola can be described as the difference of distances between a set of points, which are present in a plane to two fixed points is a positive constant. | A parabola can be described as a set of points in a plane which are equidistant from a straight line or directrix and focus. |
| Branches | A hyperbola is a disconnected curve with only one branch. | A parabola is a connected curve with only one branch. |
| Formation | A hyperbola results from intersection of the plane and the cone, but with the plane at an orientation that is not parallel to the side of the cone. | A parabola is created when a plane cuts a conical surface parallel to the side of the cone. |
| Focus Directrix | A hyperbola has two foci and two directrix. | A parabola has single focus and directrix. |
| Accentricity | A hyperbola has an accentricity value greater than one. | Parabola has an accentricity value of one. |
| Shapes | The hyperbolas can be of different shapes. | All parabolas should have the same shape irrespective of the size. |
| Curve | The hyperbola curves open more widely than that of parabolas. | The parabola curves open less widely than that of hyperbola. |
| Number Of Curves | The hyperbola has two curves that mirror each other and open in opposing sides. | The parabola has only one curve. |
| Asymptotes | A hyperbola has two asymptotes. | A parabola has no asymptotes. |
| Arms | The arms present in hyperbola are not parallel to each other. | The two arms present in a parabola should be parallel to each other. |
| Equation | The general equation of a hyperbola is written as x2/a2-y2/b2=1 | The general equation of a parabola is y=ax2. |
| Application | Hyperbolas are used in various applications in today’s world including the path followed by the shadow of a sundial, the shape of an open orbit, it is also used as an arch in many construction buildings, as equations in mathematics, physics, engineering, geometry etc. | Parabolas are used in various applications such as automobile headlight reflectors, design of ballistic missiles etc. They also play a major role in physics, engineering, mathematics etc. |
Description Of Terms
- Directrix– The line perpendicular to the axis of symmetry of a parabola; a line such that the ratio of the distance between the points on the conic and the focus to the distance to the directrix is constant.
- Focus (of a parabola)– A fixed point in the interior of a parabola that lies on the axis of symmetry.
- Lactus rectum– The line segment that passes through the focus of a parabola parallel to the directrix, with endpoints on the parabola.
- Parabola- A parabola is the set of all points (x, y) in a plane that are the same distance from a fixed line, called the directrix and a fixed point (the focus) not on the directrix.